How does an air bearing work?
Many describe the air bearing gap figuratively as an air cushion between bearing and counterpart (e.g. shaft), which is generally correct, but described too statically. In and precisely because of the bearing gaps, which are only a few micrometers thick, dynamic processes such as squeeze film dampers, shear flows and aerodynamic effects play the dominant role and generate gap flow velocities (without any movement of the bearing pairs) of more than 250 m/s. Thus, a pressurized system described in layman’s terms has little in common with an air bearing.
We distinguish between aerodynamic and aerostatic bearings, whereby the bearing pressure in the former is generated solely by the relative motion of the bearing pairs themselves, which have special features such as elevations and/or structures for this purpose. Fig. 11 shows a sectional view of a static and aerodynamic radial bearing without shaft as a striking example. For aerostatic bearings, the bearing pressure must be introduced into the bearing gap from the outside. For static air bearings, the bearing gap is therefore abstractly the gap system between the outlet and inlet and is dependent on these in many respects and, above all, dynamically.
The bearing function is based on the axial and tangential pressure distribution, which generates load capacity, as well as the air flow through the bearing gap, which is mainly responsible for generating stiffness. Stiffness here corresponds to the change in load carrying capacity with the radial displacement of the shaft (radial bearings) or the axial displacement of the plate (thrust bearings). The pressure distribution as well as the flow rate, however, are sometimes functions of the bearing gap as well as the throttling, whereby a distinction is made here between throttling at the inlet (inlet throttled) or at the outlet (outlet throttled).
Reduction - Why necessary?
The following example will be used to discuss why a reduction in the feed pressure into the bearing gap of a static air bearing is so important and critical to performance.
In example 12a, the shaft between the upper and lower bearing edges is in geometric as well as physical equilibrium. There is pressure pm=pm1=pm2 all around between the rows of nozzles. Due to a disturbance – for example cutting force – the shaft is now displaced according to 12b and creates gaps of different sizes H1 and H2.
If the feed pressure P0 were now directed into the bearing gap without being throttled, the same pressure and thus force would prevail over the circumference everywhere. A restoring force against the “disturbance” would therefore be missing, the bearing would have no function.
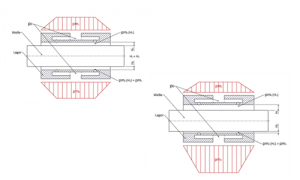
Through analytically and iteratively calculated and optimized nozzles – fed by the feed pressure p0 – an intermediate pressure pm (H,p0…) is generated after the nozzle, which is sometimes dependent on the bearing gap thickness H immediately after the nozzle. Ergo, the smaller the bearing gap after the respective nozzle, the higher the intermediate pressure pmafter the nozzle and thus also the pressure force.Thus, in the event of a displacement of the shaft by disturbance, a path-dependent restoring force and thus also stiffness – i.e. restoring force change with displacement – is ensured.